At each age, tables such as table 1, provide 4 independent
ratios, 
, i,j=1,2. If we assume that the 4 unknown
forces are constant during 
, we may estimate these forces.
T is the interval between two rounds, i.e. about 2 years.
Matrix 
from equation 1 can be diagonalized; the
eigenvalues are the roots of equation:
Since:
,
this equation leads to 2
distinct real and negative roots, 
and 
, r>s, where:
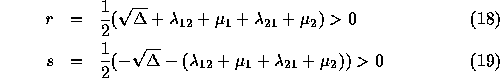
Therefore, 
, or the probability for an individual in
state j at time 0 to be in state k at time t, can be written:
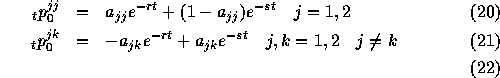
Constants are determined by initial conditions at time 0:
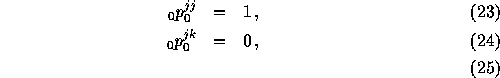
and by conditions which derivates at time 0 must satisfy:
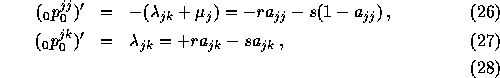
This leads to:
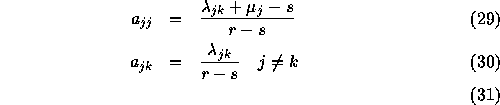
Since 
, the expression
can also be written:
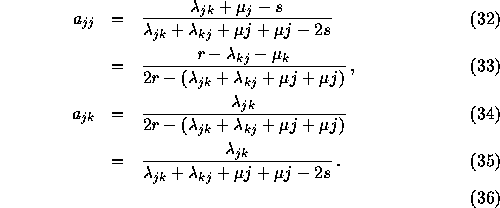
If 
corresponds to the (
) matrix with element
, it can be written
:
As 
is known from the LSOA survey for each single age, this
leads to a system of four equations with four unknowns,
, 
, 
and 
.
For the numeric calculations we used IMSL dneqnf subroutine.
As T is about 2 years, we can either use single age or double age
(x, x+2) estimates.