An approximation of the time that individuals can expect to spend in a given health state

 

Usually the Sullivan index is interpreted as an estimate of the time individuals will be likely to spend in a particular health state before death. This notion is supposed to generalize that of life expectancy [6].

Finding the life expectancy , whether for a cohort or from a current life table, is a familiar calculation. However, using a current life table leads to calculate what a person could expect to live in the future if all the age specific death rates observed at a particular date remain the same in the future. In the same way, what is called health expectancy is the expected time spent in an health state if the age-specific incidence rates between all the different health states remain the same. So, to generalize the idea of a period life expectancy (calculated with a current life table and assuming the stability of mortality rates that is to say stability of incidence rates of mortality), we have to build a multi-state life table based on the stability of all incidence rates.

Then, the calculation of health expectancies is assumed to follow similar lines as life expectancy. The life expectancy at age x is the future person years lived divided by the number of survivors, that is,

 

For example, in the simplest case of two states called Disability free (abbreviated DF) and Disabled (D), the two health expectancies at age x likely to be computerized are defined by:

1. Heath expectancy of the DF state

   

2. Health expectancy of the D state

   

where and are the numbers of person years lived from age x onwards on the states DF and D respectively.

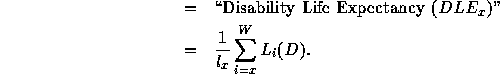
The central problem is the calculation of the person years spent in the given states of health. Multi-state longitudinal data is required to count the transition rates between states and the time spent in them. When they exist, they usually come from a longitudinal survey with at least two rounds separated by one or several years (according to the survey). However, frequently data of this detail is not available.

Then, using the Sullivan method as an approximation of health expectancy (multi-state) leads to do the hypotheses that:

These hypotheses are obviously questionable in two particular cases:

1. When prevalence ratios remain the same between two periods whereas incidence rates between states of health change rapidly. For example, Sullivan method may underestimate (or overestimate) health expectancy, because the prevalence measures of bad health at a given age in the population reflect past probabilities of becoming ill at each younger age [7].
2. On the opposite, when prevalence ratios change (for example, because of decrease of mortality) whereas incidence rates between states of health remain stable over time, the two methods may lead to different results [1].

In one of these two cases, Sullivan and Multi-state methods have different meanings. For example, in the first, Sullivan indicator fails to be a good predictor of changes in the years an individual can expect to live healthy (for example) but remains a meaningful indicator of the state of health of a population at a starting point in time. In any case, to distinguish what is provided by Sullivan index from what would be provided by multi-state approach, it is said that Sullivan healthy life expectancy (for example) reflects the healthy years an individual can expect to live if current patterns of prevalences apply during an entire lifetime.

Otherwise, there are particular occasions where the two methods lead to close results:

• For example, Sullivan index would be a good approximation for multi-state index if the illness under consideration satisfies certain properties over time. For example, if a three-state Markov process can be assumed to govern movements among the states and if the recovery rates from illness are large[8].
• Furthermore, it seems that Sullivan method would also provide a close estimate of the multi-state value of health expectancy if changes in all transition rates are sufficiently smooth and regular over time [14].

On a more general way, many researchers have described and commented the practical differences between the Sullivan and Multi-state methods. The reader can refer (for example) to: [12], [16], [13], [2], [7], [19],  [23].